Integer square root

In number theory, the integer square root (isqrt) of a non-negative integer n is the non-negative integer m which is the greatest integer less than or equal to the square root of n, $${\displaystyle \operatorname {isqrt} (n)=\lfloor {\sqrt {n}}\rfloor .}$$

For example, ${\displaystyle \operatorname {isqrt} (27)=\lfloor {\sqrt {27}}\rfloor =\lfloor 5.19615242270663...\rfloor =5.}$

Introductory remark

Let ${\displaystyle y}$ and ${\displaystyle k}$ be non-negative integers.

Algorithms that compute (the decimal representation of) ${\displaystyle {\sqrt {y}}}$ run forever on each input ${\displaystyle y}$ which is not a perfect square.

Algorithms that compute ${\displaystyle \lfloor {\sqrt {y}}\rfloor }$ do not run forever. They are nevertheless capable of computing ${\displaystyle {\sqrt {y}}}$ up to any desired accuracy ${\displaystyle k}$.

Choose any ${\displaystyle k}$ and compute ${\textstyle \lfloor {\sqrt {y\times 100^{k}}}\rfloor }$.

For example (setting ${\displaystyle y=2}$): $${\displaystyle {\begin{aligned}&k=0:\lfloor {\sqrt {2\times 100^{0}}}\rfloor =\lfloor {\sqrt {2}}\rfloor =1\\&k=1:\lfloor {\sqrt {2\times 100^{1}}}\rfloor =\lfloor {\sqrt {200}}\rfloor =14\\&k=2:\lfloor {\sqrt {2\times 100^{2}}}\rfloor =\lfloor {\sqrt {20000}}\rfloor =141\\&k=3:\lfloor {\sqrt {2\times 100^{3}}}\rfloor =\lfloor {\sqrt {2000000}}\rfloor =1414\\&\vdots \\&k=8:\lfloor {\sqrt {2\times 100^{8}}}\rfloor =\lfloor {\sqrt {20000000000000000}}\rfloor =141421356\\&\vdots \\\end{aligned}}}$$

Compare the results with ${\displaystyle {\sqrt {2}}=1.41421356237309504880168872420969807856967187537694...}$

It appears that the multiplication of the input by ${\displaystyle 100^{k}}$ gives an accuracy of k decimal digits.

To compute the (entire) decimal representation of ${\displaystyle {\sqrt {y}}}$, one can execute ${\displaystyle \operatorname {isqrt} (y)}$ an infinite number of times, increasing ${\displaystyle y}$ by a factor ${\displaystyle 100}$ at each pass.

Assume that in the next program (${\displaystyle \operatorname {sqrtForever} }$) the procedure ${\displaystyle \operatorname {isqrt} (y)}$ is already defined and — for the sake of the argument — that all variables can hold integers of unlimited magnitude.

Then ${\displaystyle \operatorname {sqrtForever} (y)}$ will print the entire decimal representation of ${\displaystyle {\sqrt {y}}}$.

The conclusion is that algorithms which compute isqrt() are computationally equivalent to algorithms which compute sqrt().

Basic algorithms

The integer square root of a non-negative integer ${\displaystyle y}$ can be defined as $${\displaystyle \lfloor {\sqrt {y}}\rfloor =x:x^{2}\leq y<(x 1)^{2},x\in \mathbb {N} }$$

For example, ${\displaystyle \operatorname {isqrt} (27)=\lfloor {\sqrt {27}}\rfloor =5}$ because ${\displaystyle 6^{2}>27{\text{ and }}5^{2}\ngtr 27}$.

Algorithm using linear search

The following C programs are straightforward implementations.

Linear search using addition

In the program above (linear search, ascending) one can replace multiplication by addition, using the equivalence $${\displaystyle (L 1)^{2}=L^{2} 2L 1=L^{2} 1 \sum _{i=1}^{L}2.}$$

Algorithm using binary search

Linear search sequentially checks every value until it hits the smallest ${\displaystyle x}$ where ${\displaystyle x^{2}>y}$.

A speed-up is achieved by using binary search instead. The following C-program is an implementation.

Numerical example

For example, if one computes ${\displaystyle \operatorname {isqrt} (2000000)}$ using binary search, one obtains the ${\displaystyle [L,R]}$ sequence $${\displaystyle {\begin{aligned}&[0,2000001]\rightarrow [0,1000000]\rightarrow [0,500000]\rightarrow [0,250000]\rightarrow [0,125000]\rightarrow [0,62500]\rightarrow [0,31250]\rightarrow [0,15625]\\&\rightarrow [0,7812]\rightarrow [0,3906]\rightarrow [0,1953]\rightarrow [976,1953]\rightarrow [976,1464]\rightarrow [1220,1464]\rightarrow [1342,1464]\rightarrow [1403,1464]\\&\rightarrow [1403,1433]\rightarrow [1403,1418]\rightarrow [1410,1418]\rightarrow [1414,1418]\rightarrow [1414,1416]\rightarrow [1414,1415]\end{aligned}}}$$

This computation takes 21 iteration steps, whereas linear search (ascending, starting from ${\displaystyle 0}$) needs 1414 steps.

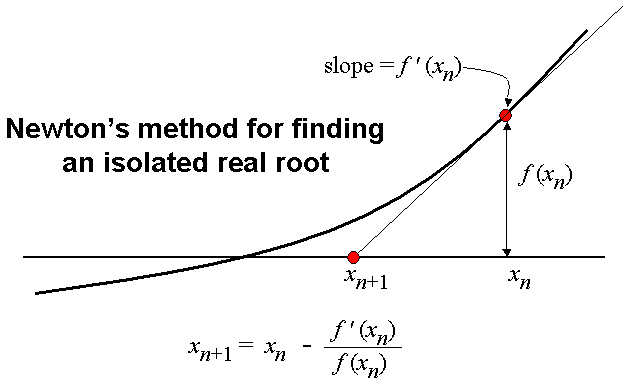
Algorithm using Newton's method

One way of calculating ${\displaystyle {\sqrt {n}}}$ and ${\displaystyle \operatorname {isqrt} (n)}$ is to use Heron's method, which is a special case of Newton's method, to find a solution for the equation ${\displaystyle x^{2}-n=0}$, giving the iterative formula $${\displaystyle x_{k 1}={\frac {1}{2}}\!\left(x_{k} {\frac {n}{x_{k}}}\right),\quad k\geq 0,\quad x_{0}>0.}$$

The sequence ${\displaystyle \{x_{k}\}}$ converges quadratically to ${\displaystyle {\sqrt {n}}}$ as ${\displaystyle k\to \infty }$.

Stopping criterion

One can prove that ${\displaystyle c=1}$ is the largest possible number for which the stopping criterion $${\displaystyle |x_{k 1}-x_{k}|$$ ensures ${\displaystyle \lfloor x_{k 1}\rfloor =\lfloor {\sqrt {n}}\rfloor }$ in the algorithm above.

In implementations which use number formats that cannot represent all rational numbers exactly (for example, floating point), a stopping constant less than 1 should be used to protect against round-off errors.

Domain of computation

Although ${\displaystyle {\sqrt {n}}}$ is irrational for many ${\displaystyle n}$, the sequence ${\displaystyle \{x_{k}\}}$ contains only rational terms when ${\displaystyle x_{0}}$ is rational. Thus, with this method it is unnecessary to exit the field of rational numbers in order to calculate ${\displaystyle \operatorname {isqrt} (n)}$, a fact which has some theoretical advantages.

Using only integer division

For computing ${\displaystyle \lfloor {\sqrt {n}}\rfloor }$ for very large integers n, one can use the quotient of Euclidean division for both of the division operations. This has the advantage of only using integers for each intermediate value, thus making the use of floating point representations of large numbers unnecessary. It is equivalent to using the iterative formula $${\displaystyle x_{k 1}=\left\lfloor {\frac {1}{2}}\!\left(x_{k} \left\lfloor {\frac {n}{x_{k}}}\right\rfloor \right)\right\rfloor ,\quad k\geq 0,\quad x_{0}>0,\quad x_{0}\in \mathbb {Z} .}$$

By using the fact that $${\displaystyle \left\lfloor {\frac {1}{2}}\!\left(x_{k} \left\lfloor {\frac {n}{x_{k}}}\right\rfloor \right)\right\rfloor =\left\lfloor {\frac {1}{2}}\!\left(x_{k} {\frac {n}{x_{k}}}\right)\right\rfloor ,}$$

one can show that this will reach ${\displaystyle \lfloor {\sqrt {n}}\rfloor }$ within a finite number of iterations.

In the original version, one has ${\displaystyle x_{k}\geq {\sqrt {n}}}$ for ${\displaystyle k\geq 1}$, and ${\displaystyle x_{k}>x_{k 1}}$ for ${\displaystyle x_{k}>{\sqrt {n}}}$. So in the integer version, one has ${\displaystyle \lfloor x_{k}\rfloor \geq \lfloor {\sqrt {n}}\rfloor }$ and ${\displaystyle x_{k}\geq \lfloor x_{k}\rfloor >x_{k 1}\geq \lfloor x_{k 1}\rfloor }$ until the final solution ${\displaystyle x_{s}}$ is reached. For the final solution ${\displaystyle x_{s}}$, one has ${\displaystyle \lfloor {\sqrt {n}}\rfloor \leq \lfloor x_{s}\rfloor \leq {\sqrt {n}}}$ and ${\displaystyle \lfloor x_{s 1}\rfloor \geq \lfloor x_{s}\rfloor }$, so the stopping criterion is ${\displaystyle \lfloor x_{k 1}\rfloor \geq \lfloor x_{k}\rfloor }$.

However, ${\displaystyle \lfloor {\sqrt {n}}\rfloor }$ is not necessarily a fixed point of the above iterative formula. Indeed, it can be shown that ${\displaystyle \lfloor {\sqrt {n}}\rfloor }$ is a fixed point if and only if ${\displaystyle n 1}$ is not a perfect square. If ${\displaystyle n 1}$ is a perfect square, the sequence ends up in a period-two cycle between ${\displaystyle \lfloor {\sqrt {n}}\rfloor }$ and ${\displaystyle \lfloor {\sqrt {n}}\rfloor 1}$ instead of converging.

Example implementation in C

Numerical example

For example, if one computes the integer square root of 2000000 using the algorithm above, one obtains the sequence $${\displaystyle {\begin{aligned}&1000000\rightarrow 500001\rightarrow 250002\rightarrow 125004\rightarrow 62509\rightarrow 31270\rightarrow 15666\rightarrow 7896\\&\rightarrow 4074\rightarrow 2282\rightarrow 1579\rightarrow 1422\rightarrow 1414\rightarrow 1414\end{aligned}}}$$ In total 13 iteration steps are needed. Although Heron's method converges quadratically close to the solution, less than one bit precision per iteration is gained at the beginning. This means that the choice of the initial estimate is critical for the performance of the algorithm.

When a fast computation for the integer part of the binary logarithm or for the bit-length is available (like e.g. std::bit_width in C 20), one should better start at $${\displaystyle x_{0}=2^{\lfloor (\log _{2}n)/2\rfloor 1},}$$ which is the least power of two bigger than ${\displaystyle {\sqrt {n}}}$. In the example of the integer square root of 2000000, ${\displaystyle \lfloor \log _{2}n\rfloor =20}$, ${\displaystyle x_{0}=2^{11}=2048}$, and the resulting sequence is $${\displaystyle 2048\rightarrow 1512\rightarrow 1417\rightarrow 1414\rightarrow 1414.}$$ In this case only four iteration steps are needed.

Digit-by-digit algorithm

The traditional pen-and-paper algorithm for computing the square root ${\displaystyle {\sqrt {n}}}$ is based on working from higher digit places to lower, and as each new digit pick the largest that will still yield a square ${\displaystyle \leq n}$. If stopping after the one's place, the result computed will be the integer square root.

Using bitwise operations

If working in base 2, the choice of digit is simplified to that between 0 (the "small candidate") and 1 (the "large candidate"), and digit manipulations can be expressed in terms of binary shift operations. With * being multiplication, << being left shift, and >> being logical right shift, a recursive algorithm to find the integer square root of any natural number is:

Traditional pen-and-paper presentations of the digit-by-digit algorithm include various optimizations not present in the code above, in particular the trick of pre-subtracting the square of the previous digits which makes a general multiplication step unnecessary. See Methods of computing square roots § Binary numeral system (base 2) for an example.

Karatsuba square root algorithm

The Karatsuba square root algorithm is a combination of two functions: a public function, which returns the integer square root of the input, and a recursive private function, which does the majority of the work.

The public function normalizes the actual input, passes the normalized input to the private function, denormalizes the result of the private function, and returns that.

The private function takes a normalized input, divides the input bits in half, passes the most-significant half of the input recursively to the private function, and performs some integer operations on the output of that recursive call and the least-significant half of the input to get the normalized output, which it returns.

For big-integers of "50 to 1,000,000 digits", Burnikel-Ziegler Karatsuba division and Karatsuba multiplication are recommended by the algorithm's creator.

An example algorithm for 64-bit unsigned integers is below. The algorithm:

1. Normalizes the input inside u64_isqrt.
2. Calls u64_normalized_isqrt_rem, which requires a normalized input.
3. Calls u32_normalized_isqrt_rem with the most-significant half of the normalized input's bits, which will already be normalized as the most-significant bits remain the same.
4. Continues on recursively until there's an algorithm that's faster when the number of bits is small enough.
5. u64_normalized_isqrt_rem then takes the returned integer square root and remainder to produce the correct results for the given normalized u64.
6. u64_isqrt then denormalizes the result.

In programming languages

Some programming languages dedicate an explicit operation to the integer square root calculation in addition to the general case or can be extended by libraries to this end.

See also

• Methods of computing square roots

Notes

References

External links